CLASE2

 FECHA :  04 - 12 - 2020

TEMA:  Impulso 

https://www.youtube.com/watch?v=mes4Ui0NdFc

El impulso mecánico, de una fuerza ,  es una magnitud vectorial que relaciona dicha fuerza con el tiempo que dura su actuación.

I→=F→⋅Δt

Donde:

• I→: Es el impulso mecánico de la fuerza. Su unidad en el Sistema Internacional (S.I.) es el newton por segundo ( N·s )
• F→: Es la fuerza que estamos considerando, supuesta constante. Su unidad de medida en el S.I. es el newton ( N )
• Δt: Es el intervalo de tiempo durante el cual actúa la fuerza. Su unidad de medida en el S.I. es el segundo ( s )

Observa que, de la definición anterior se deduce que el vector impulso de una fuerza posee la misma dirección y sentido que la fuerza a la que está asociado.

Teorema del impulso mecánico

Teniendo en cuenta que, tal y como hemos visto en la segunda ley de Newton, la variación de la cantidad de movimiento o momento lineal se puede relacionar con la fuerza resultante que actúa sobre un cuerpo según:

F→=Δp→Δt⇒F→⋅Δt = Δp→

El producto F→⋅Δt es la propia definición que hemos dado para el impulso mecánico, con lo que este queda relacionado con la variación del momento lineal del cuerpo. Se trata del teorema del impulso mecánico.

El teorema del impulso mecánico establece que el impulso mecánico de la fuerza resultante que actúa sobre un cuerpo es igual a la variación de su momento lineal:

I→=F→⋅Δt =Δp→

Donde:

• I→: Es el impulso mecánico total al que se encuentra sometido el cuerpo, es decir, el impulso de la fuerza resultante. Su unidad en el Sistema Internacional (S.I.) es el newton por segundo ( N·s )
• F→: Es la fuerza resultante o fuerza total a la que se encuentra sometido el cuerpo, supuesta constante. Su unidad de medida en el S.I. es el newton ( N )
• Δt: Es el intervalo de tiempo durante el cual actúa la fuerza. Su unidad de medida en el S.I. es el segundo ( s )
• Δp→: Representa la variación del momento lineal producida en el intervalo de tiempo considerado. Se puede calcular como la diferencia entre su valor final y su valor inicial: Δp→=p→f−p→i, y recuerda que p→=m⋅v→. Su unidad de medida en el S.I. es el kg·m/s.

Observa que la expresión anterior pone de manifiesto la afirmación que hicimos de que para conferir una determinada velocidad a un cuerpo (aumentar su momento lineal) podemos actuar de dos formas: actuar sobre la fuerza o sobre el tiempo durante el cual actúa. Así, en los transbordadores espaciales la nave alcanza la velocidad deseada debido al efecto continuado de la fuerza que proporcionan los propulsores.

Aunque están estrechamente relacionados, no debes confundir el momento lineal con el impulso mecánico. Este último se puede relacionar con la variación del primero, pero son magnitudes conceptualmente distintas.

Efectivamente, es común que se produzcan ciertas confusiones. Ten presente que, al fin y al cabo, sus ecuaciones de dimensiones son las mismas...

[I]=M⋅L⋅T−1

...y las unidades de medida en el S.I. son equivalentes...

N⋅s≡m⋅s−1

Ejemplo

Un cuerpo de 1 kg se encuentra sometido a una única fuerza F→=−6 ⋅i→ +8⋅j→ N durante 5 s. Sabiendo que su velocidad inicial es vo→=15 ⋅i→ −10⋅j→ N. Calcula:

a) El impulso mecánico
b) El momento lineal antes y después de aplicar la fuerza.

Fuerzas variables

En la definición que hemos hecho de impulso lineal asumimos que la fuerza permanece constante durante el intervalo de tiempo ∆t que actúa. En general esto no es así, sino que la fuerza es variable. Podemos entonces buscar el impulso que actúa sobre un intervalo de tiempo infinitamente pequeño (diferencial). Dicho impulso sería entonces un impulso diferencial, y la fuerza que actuaría sobre dicho intervalo de tiempo si que sería constante. Utilizando notación diferencial nos queda:

dI→=F→⋅dt

Con lo que el impulso transferido durante un intervalo de tiempo finito se obtiene sumando los infinitos impulsos diferenciales, es decir, integrando:

∫tftidI→=∫tftiF→⋅dt⇒I→=∫tftiF→⋅dt

En cuanto al teorema del impulso, observa que podemos llegar al mismo enunciado ya presentado para fuerzas constantes, considerando esta vez fuerzas variables. Para comprobarlo debemos considerar la versión diferencial de la segunda ley de Newton, es decir, F→=dp→dt . Así, nos queda:

I=∫tftiF→⋅dt=∫tftidp→dt⋅dt=∫tftidp→=[p→]tfti=p→f−p→i=Δp→

Gráficas de impulso

Es probable que a estas altura de tus estudios ya sepas que la integral definida entre dos valores de una función coincide numéricamente en valor con el área encerrada bajo dicha función. Así, si representamos en el eje horizontal el tiempo y en el eje vertical la fuerza, ya sea constante o variable, el área encerrada bajo la curva entre ti y tf coincide con el valor del impulso:

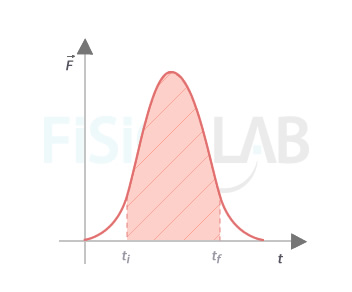
Cálculo de impulso

En la gráfica se representa como varía la fuerza que actúa sobre un cuerpo cualquiera a lo largo del tiempo. El área encerrada bajo la curva entre los instantes ti y tf, rayada en rojo, coincide numéricamente con el valor del impulso de dicha fuerza en el intervalo tf - ti, y por tanto con el valor de la variación del momento lineal que experimentará el cuerpo sobre el que se aplique en dicho intervalo.

A partir de esta idea, observa que siempre es posible encontrar una fuerza promedio constante cuyo valor de impulso en ese intervalo de tiempo coincida con el de la fuerza variable.

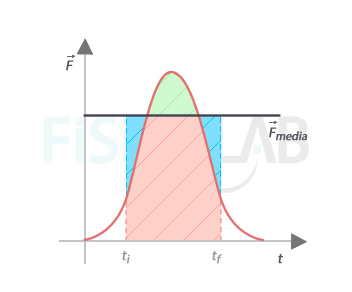
Fuerza media constante

Dado que el área rayada en azul y la rayada en verde son iguales, él área encerrada bajo la curva roja que representa la fuerza real y variable coincide con el área encerrada bajo la curva de la fuerza promedio F→media, representada en negro. Al tratarse del área de un rectángulo, el cálculo de esta última se reduce a una simple multiplicación F→media⋅(tf−ti), frente al uso de integrales que requeriría la primera.

Por tanto, en la mayoría de los casos y problemas que abordaremos en este nivel, cuando hablemos del impulso de una fuerza nos referiremos a dicha fuerza media supuesta constante.